知言 / CS336 Assignment1部分作业

Transformer概述

以原始Transformer为例，讲解一遍其中的子层和各部分有什么用：

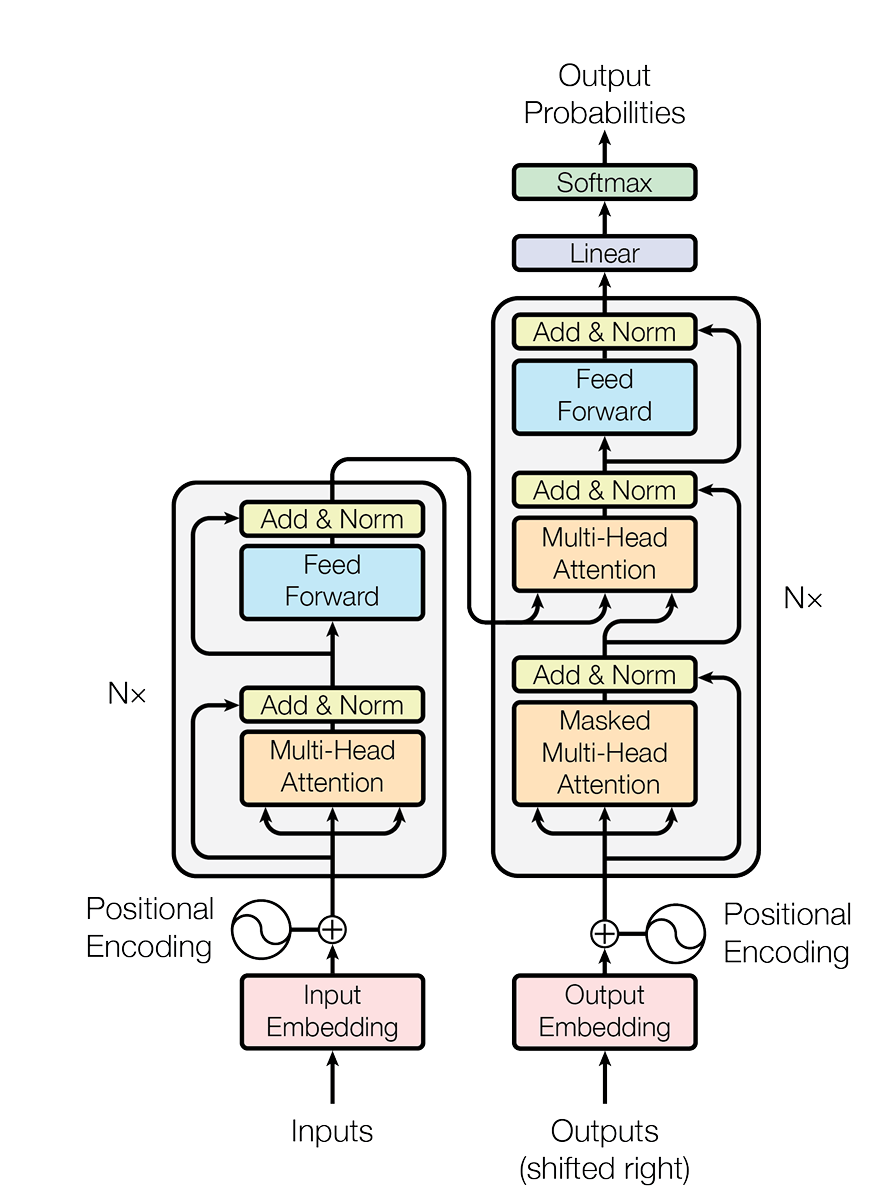
1. 注意力机制 此部分是Transformer核心中的核心，指代的图中的橙色部分，大致分为三类：多头自注意力机制，masked多头注意力机制，交叉注意力（cross attention）机制。 注意力的核心是构建：
   • Query 问询矩阵，这个矩阵会包含“需要获得什么信息”
   • Key 键矩阵，这个矩阵会包含“句子有什么信息能被检索”
   • Value 值矩阵，这个矩阵会包含“句子能提供什么信息”
   • 以上三个矩阵是由$W^Q/W^K/W^V \cdot X$得到，X是输入的信息 多头会在实现注意力机制的时候详细讲解，自注意是指在encoding中所有上述三个值都由Inputs获得，交叉注意力是指decoding中K和V矩阵是由encoder给出，Q是由decoder的masked注意力机制给出。masked注意力机制是因为在训练中是要给出outputs的完整序列，若是decoder能看到将要预测的信息，则训练没有意义，所以在decoder的output上加了mask机制
2. Tokenization&embedding 简而言之，这两者是将由utf-8编码的文字转为便于训练的数字并投影到一个连续的向量空间中。具体实现见后文。
3. 前馈神经网络&归一化 但是注意力机制本质上就是线性混合，并没有强大的非线性表达能力，加上一层神经网络，可以大大增强其非线性表达能力。而归一化则防止了梯度爆炸和梯度消失，更有利于模型训练。 同时模型设计了残差连接，即输入神经网络和归一化层的x会加在这个层的输出上，这样同样缓解梯度爆炸/消失，有利于模型优化
4. 最后加上一层线性函数和softmax，在词表中选取输出的词汇。

整整50页的handout😰，先通读一遍，洋文怎么那么难懂。 整个assignment要求实现：

• 一个BPE分词器(tokenizer)
• transformer语言模型
• 交叉熵损失函数和AdamW优化器
• 训练函数 assignment给出了一些数据以供学习，目前不知道训练能不能用消费级GPU完成，不排除要租算力的可能。

禁止使用torch.nn, torch.nn.functional, or torch.optim这些类，除了：

• torch.nn.Parameter
• Container classes in torch.nn (e.g., Module, ModuleList, Sequential, etc.) 见官方文档以见container类
• torch.optim.Optimizer base class

要求完成：

• cs336_basics/*：所有code都要继承在这个文件夹下，具体实现可自由发挥。
• adapters.py：要求必须在你的函数中实现这个文件中的所有接口，通过调用手搓的函数来完善这个文件，这是用于调用所写函数的“胶水代码“
• test_*.py：要通过的所有测试。

Tokenizer

UTF-8 编码方式

训练方式

作业提出需要使用BPE方式进行分词训练，主要有以下三步：

1. Pre-tokenization：如果此时开始merge的话便会导致标点对分词产生影响，导致分出两个词义相差无几却分成不同词的情况，所以GPT-2的实践形式是先用正则化分出标点和单词，分别进行分词，导致标点不影响分词。

1
2
3
4

>>> PAT = r"""'(?:[sdmt]|ll|ve|re)| ?\p{L}+| ?\p{N}+| ?[^\s\p{L}\p{N}]+|\s+(?!\S)|\s+"""
>>> # requires `regex` package 
>>> import regex as re 
>>> re.findall(PAT, "some text that i'll pre-tokenize") ['some', ' text', ' that', ' i', "'ll", ' pre', '-', 'tokenize']

2. 词汇初始化：将所有词汇按照UTF-8的编码转为原码，之后按照字节进行拆分，由于一个字节大小是256，所以初始的词汇表是256.
3. 训练分词器：依照频数对最高的词进行融合 注意：需要对<|endoftext|>这个特殊的字符进行分词，并保证分词不变。

提升性能 分词可能很慢，可以通过multiprocessing这个自带库进行并行计算加快pre-tokenization这步，可以查看实例来学习 提前分词 需要把<|endoftext|>纳入考虑，可以用re.split分为两个文本后用|连接起来。

优化

吭哧吭哧做完了，在自己的测试上跑通了，但是在官方测试上超时了😭 改进：

1. 用int将bytes替换，在最后输出时再替换为byte。每合并一个字符就给这个字符赋予一个新的id，最后用这个字典将id转为bytes，同时在运行过程中维护这样的字典。按照gpt所说，这应该能让我勉强过线，先试试看🤓
2. 实际不行，检测每步操作时间。

   1 2 3 4 5

   Time to delete words: 0.02 seconds Time to encode text: 0.01 seconds Time to train BPE: 5.96 seconds Time to find most frequent pair: 0.02 seconds Time to merge byte sequences: 0.02 seconds

   可以发现性能瓶颈主要在训练上，虽然每一次删除和融合速度都较快，但是数百次融合和求最多字符对导致时间累计得很大。因此，改为采用最大堆和惰性校验方法。
   • 原始方式：先遍历整个token库O(N)，找到最多的token对，然后遍历整个token库把这个token对merge掉O(N) 。
   • 半优化方式：在最开始统计seq_pair O(N)，然后维护一个最大堆，每次循环从最大堆中选取最大的token对，并和seq_pair比较，数量相同才选取，然后merge他两并惰性遍历整个token库得到部分更新的seq_pair
   • 实际上还有业界的最优化算法，貌似挺复杂的暂时不采用。 需要更新的函数：

• 整个train_bpe()
• merge的时候同时惰性更新seq_pair
• 增加最大堆。 注意：当多个token对对数并列时，选取字典序数最大的那个 成功使得运行时间控制到1s左右。 但是在后期merge仍然有冲突，猜测可能是并列的时候没有处理好导致的，无力再修了，直接在网上抄个答案(结果有的也有问题……)。 stanford-cs336-a1/cs336_basics/BPETokenizer.py at main · Spectual/stanford-cs336-a1 这个是没问题的。一个分词器就写了三天…… 接下来是Transformer的核心组件：embedder，encoder，decoder，softmax等

Transformer Language Model Architecture

现在的语言大模型不同于Ateention is all you need中的架构，一般都是先进行归一化，输入encoder后再进入残差神经网络。语言大模型接受(batch_size, sequence_length)维度的输入，之后输出(batch_size, sequence_length, vocab_size)大小的输出，取其中概率最高的词作为lm下一个输出的词，然后用实际的下一个词计算交叉熵损失。 以下列举一些lm的模块：

• embedder transformer把一系列token ID转为连续的向量，具体的是把(batch_size, sequnce_langth)的向量转为(batch_size, sequence_length, d_model)
• 归一化前的transformer模块 经过num_layers个Transformer层，我们会把最终的结果转为词的分布。现在的实现是把归一化放在encoder后的，归一化后，我们将使用一个标准的训练过的线性转化把输出转为预测下一个token的向量。

Torch中的行/列向量与广播机制

行向量 (row vector) 数学上是形状 [1, n]，一行 n 列。

常见写法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

import torch

# 一维向量 (等价于行向量，会自动广播)
row1 = torch.tensor([1., 2., 3.])        # shape: [3]

# 显式行向量
row2 = torch.tensor([[1., 2., 3.]])      # shape: [1, 3]

print(row1.shape)  # torch.Size([3])
print(row2.shape)  # torch.Size([1, 3])

✅ 在矩阵加法中，这两者都会表现为「行向量」，差别只是 row1 是一维，row2 是二维。

列向量 (column vector)

数学上是形状 [n, 1]，n 行一列。

常见写法

1
2
3
4
5
6
7
8
9

# 显式列向量
col = torch.tensor([[1.], [2.], [3.]])  # shape: [3, 1]

# 或者把行向量转置
row = torch.tensor([[1., 2., 3.]])      # shape: [1, 3]
col2 = row.T                            # shape: [3, 1]

print(col.shape)   # torch.Size([3, 1])
print(col2.shape)  # torch.Size([3, 1])

用 unsqueeze / view 控制维度

如果你一开始是 一维向量 [n]，可以用这些方法转为行/列向量：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

v = torch.arange(1, 4)     # shape: [3] = [1, 2, 3]

# 行向量
row = v.unsqueeze(0)       # [1, 3]

# 列向量
col = v.unsqueeze(1)       # [3, 1]

print(row.shape)  # torch.Size([1, 3])
print(col.shape)  # torch.Size([3, 1])

广播机制 为了出发广播机制，进行运算的张量必须满足以下条件：

• 每个张量至少有一个维度。
• 迭代维度尺寸时，从尾部的维度开始，维度尺寸
  • 或者相等，
  • 或者其中一个张量的维度尺寸为 1 ，
  • 或者其中一个张量不存在这个维度。 示例：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 示例5：可广播
c = torch.empty(5, 1, 4, 1)
d = torch.empty(   3, 1, 1)
(c + d).size()  # torch.Size([5, 3, 4, 1])


# 示例6：可广播
f = torch.empty(      1)
g = torch.empty(3, 1, 7)
(f + g).size()  # torch.Size([3, 1, 7])


# 示例7：不可广播
o = torch.empty(5, 2, 4, 1)
u = torch.empty(   3, 1, 1)
(o + u).size()

# 报错：
# ---------------------------------------------------------------------------
#
# RuntimeError                              Traceback (most recent call last)
#
# <ipython-input-17-72fb34250db7> in <module>()
#       1 o=torch.empty(5,2,4,1)
#       2 u=torch.empty(3,1,1)
# ----> 3 (o+u).size()
#
# RuntimeError: The size of tensor a (2) must match the size of tensor b (3) at non-singleton dimension 1

数学表示

对于如numpy和pytorch等数学库，通常写作的是行向量，比如创建一个Linear(in_feature, out_feature)中：

• weight.shape = (out_feature, in_feature) 所以，在线性代数中的公式$y=Wx$，在这类库中要写成$y = x @ W.T$，这样有利于调用底层的矩阵运算库。

线性模型

Assignment要求实现一个线性模型，实现：

• def __init__(self, in_features -> int, out_features -> int, device=None, dtype=None)
• def forward(self,x:torch.Tensor)->torch.Tensor 要求：
• 为nn.Module子类
• 继承父类
• 用W而非W^T来储存参数，这样更高效，并且同时用nn.Parameter包装
• 用torch.nn.init.trunc_normal_来初始化
• 不允许使用nn.Linear或nn.functional.linear 初始化：
• 线性权重：$\mathcal{N}\left(\mu=0, \sigma^{2}=\frac{2}{d_{\text{in}}+d_{\text{out}}}\right)$ 截断于 $[-3\sigma, 3\sigma]$。
• Embedding：$\mathcal{N}\left(\mu=0, \sigma^{2}=1\right)$ 截断于 $[-3, 3]$
• RMSNorm: $\mathbb{I}$(全1向量)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

flowchart LR
    subgraph Input
        X["x: [batch, in_features]"]
    end

    subgraph Parameters
        W["W: [out_features, in_features]"]
        B["b: [out_features]"]
    end

    subgraph Computation
        XT["x @ W.T → [batch, out_features]"]
        ADD["Add bias (broadcast)"]
    end

    subgraph Output
        Y["y: [batch, out_features]"]
    end

    X --> XT
    W --> XT
    XT --> ADD
    B --> ADD
    ADD --> Y

广播机制会把b:[out_features]扩展为b:[batch_size,out_features]，但是此处好像不需要设置bias项，只要求实现一个线性变化。同时注意torch的实现惯例是把W当作[out_feature,in_feature]的向量

nn.Parameter

• nn.Parameter 是 torch.Tensor 的子类。
• 它的特别之处在于：
  • 当你把 Parameter 放到一个继承自 nn.Module 的类里时，PyTorch 会自动把它注册为模型的可训练参数。
  • 这意味着：优化器（如 torch.optim.SGD、Adam）在调用 model.parameters() 时会找到它，并更新它的值。
  • 可以用于你希望在训练中被优化的张量如权重矩阵 W 和 偏置向量 b。

Embedding

参考文献：Glossary of Deep Learning: Word Embedding | by Jaron Collis | Deeper Learning | Medium，Cross-Entropy Loss Function in Machine Learning: Enhancing Model Accuracy | DataCamp Embedding层是将Tokenizer输出的id映射到d_model维度的向量空间。要求实现：

• 维度上的降维
• 语义上的近似

实际上就是一个大矩阵，把tokenizer训练的bytes2int字典中的每个token的id转化成独热编码，把独热编码输入线性网络后输出映射在向量空间上的向量。而训练则分为独立训练与和下游网络一起训练两种方式。

• 同下游网络一起训练是当下端到端的训练的常见形式
• 早期或者微调阶段的embedding也会用CBOW等方法独立训练 具体方法是用交叉熵优化模型，即： $$H(p,q) = -\Sigma_x{ p(x)\log{q(x)}}$$ 这里的$p$和$q$是概率分布，以softmax算法为例： $$ \begin{aligned} p &= [0,0,1],\quad q = [0.1,0.7,0.2]\\ H(p,q) &=-(0\times\log{0.1}+0\times\log{0.7}+1\times\log{0.2}) \end{aligned} $$ 此处要求实现：
• __init__(self, num_embeddings, embedding_dim, device=None, dtype=None): 构建一个嵌入模块。此函数应接受以下参数：
  • num_embeddings: int 词汇表的大小
  • embedding_dim: int 嵌入向量的维度，即 $d_{\text{model}}$
  • device: torch.device | None = None 存储参数的设备
  • dtype: torch.dtype | None = None 参数的数据类型
• def forward(self, token_ids: torch.Tensor) -> torch.Tensor: 查找给定 token ID 的嵌入向量。 确保：
• 继承自 nn.Module
• 调用超类构造函数
• 将你的嵌入矩阵初始化为 nn.Parameter
• 将嵌入矩阵存储为最终维度为 $d_{\text{model}}$
• 不要使用 nn.Embedding 或 nn.functional.embedding 再次使用上述设置进行初始化，并使用 torch.nn.init.trunc_normal_ 初始化权重。

预归一化Transformer模块

所有Transformer都有两个模块：多头注意力机制和前馈神经网络 在初始的Transformer中，模型在两个sub-Layersz中使用了归一化加上残差连接，现在常称为“后归一化(post-norm)”。然而研究发现使用前归一化可以有效提升模型训练稳定性。可以理解为每一个Transformer块输出的内容会不经归一化“纯净”地进行残差连接。接下来会遍历预归一化的Transformer的所有内容，一连串地实现它们。

均方根层归一化

其中$\text{RMS}(a)=\sqrt{\frac1{d_model}\sum_{i=1}^{d_model}a_i^2+\epsilon},\quad g_i\text{是一个可以学习的增益(gain)参数，而}\epsilon=1e-5$ 注：可以将参数转为torch.float32来防止溢出。比如你的forword()应该如此写：

1
2
3
4
5
6
7

in_dtype = x.dtype 
x = x.to(torch.float32) 
# Your code here performing RMSNorm 
... 
result = ... 
# Return the result in the original dtype 
return result.to(in_dtype)

同时注意输入张量的维度是[batch_size, seq_length, d_model]，求和的时候对最后一维求和。

dim参数在max, mean, sum等函数中不同参数的含义： dim为0和1时分别表示对行求和和对列求和，也可以用负数表示倒数第几个维度，比如下列向量：

1
2
3
4
5
6

x = torch.tensor([[1, 2, 3],
                  [4, 5, 6]])
x.sum(dim=0)
tensor([5, 7, 9])   # [1+4, 2+5, 3+6]
x.sum(dim=1)
tensor([ 6, 15])   # [1+2+3, 4+5+6]

同时可以使用keepdim=true来保留求和的那个维度，防止降维，这个可用于广播机制。

1
2
3
4
5

x.sum(dim=0, keepdim=True)
tensor([[5, 7, 9]])   # shape [1, 3]
x.sum(dim=1, keepdim=True)
tensor([[ 6],
        [15]])        # shape [2, 1]

前馈神经网络

其中$\odot$表示逐元素相乘，如果使用Sigmoid/tanh等激活函数，可能导致梯度消失，而ReLU等函数则可能导致恒为0的神经死亡。geting机制在使用Sigmoid函数的同时乘以了一个线性函数，把Sigmoid函数作为了一个“门控作用”。此处可以使用torch.sigmoid()函数。

注意：因为x的维度通常是[batch_size, seq_length, d_model]，要与[d_ff, d_model]的W相乘。需要运用广播机制的话，要求左张量的最后一维和右张量的倒数第二位相等，所以要x @ W.T -> [batch_size, seq_length, d_model] @ [d_model, d_ff]

相对位置Embeddings

也就是对于$i\in\{1,\cdots,seq\_len\},k\in\{1, \cdots, \frac d2\}$，则对于每个$x^i\in\mathbb{R}^d$，可以把其分为$\frac d2$组，然后对其乘上$R^i$矩阵，最后再拼接回去，得到经过position embedding的向量。(实践中k是从0开始记得，所以计算$\theta$的公式也得改)

同时会传入position数组，维度同seq_len相同，作为位置索引。 实现形式是计算一个[seq_len, d/2]的cos和sin矩阵，最后直接应用广播机制与x相乘。

点乘Softmax

但是注意到有时候$v$会过大，导致出现$\frac{\inf}{\inf}$的情况，对此，我们可以把这个向量每个元素减去最大的元素，把最大的元素变为0，可以有效缓解此现象。

• $n$：query 的序列长度（通常是目标序列的长度，比如解码时的句子长度）。
• $m$：key/value 的序列长度（通常是源序列的长度，比如输入句子的长度）。
  • 在自注意力（self-attention）中，通常 $n = m$。
  • 在交叉注意力（cross-attention，比如 encoder-decoder attention）中，$n$ 和 $m$ 可以不同。
• $d_k$：query/key 的维度。
  • Query 和 Key 必须在同一向量空间里才能计算内积（相似度）。
  • 所以它们共享同一个维度 $d_k$。
• $d_v$：value 的维度。
  • Value 不参与相似度计算，它只是被“加权平均”后输出。
  • 因此它的维度可以不同于 $d_k$，一般设为 $d_v = d_k$，但理论上可以不一样。 同时设计一个mask： $M \in {True,False}^{n×m}$，如果$M$矩阵为False,需要在此处的预softmax值加上$-\infty$。 算出来$Q^TK$之后再key维做softmax，求得要对哪个key值做注意力。

多头注意力机制

但是具体实践中建立多个单头注意力并单独计算会非常影响性能，所以普遍的实践是把多头注意力的小矩阵在参数维度叠加起来，即： $$ \begin{aligned} &\textbf{输入：} \ &\quad X \in \mathbb{R}^{n \times d_{\text{model}}}, \quad \text{其中 $n$ 为序列长度，$d_{\text{model}}$ 为 embedding 维度。} \

&\textbf{Step 1：线性投影并拆分为 $h$ 个头} \ &\quad \text{对于每个头 $i \in \{1,\dots,h\}$，定义投影矩阵：} \ &\quad W_Q^{(i)} \in \mathbb{R}^{d_{\text{model}} \times d_k}, \quad W_K^{(i)} \in \mathbb{R}^{d_{\text{model}} \times d_k}, \quad W_V^{(i)} \in \mathbb{R}^{d_{\text{model}} \times d_v}, \ &\quad \text{其中 } d_k = d_v = \frac{d_{\text{model}}}{h}. \

&\quad \text{得到每个头的投影结果：} \ &\quad Q^{(i)} = X W_Q^{(i)} \in \mathbb{R}^{n \times d_k}, \ &\quad K^{(i)} = X W_K^{(i)} \in \mathbb{R}^{m \times d_k}, \ &\quad V^{(i)} = X W_V^{(i)} \in \mathbb{R}^{m \times d_v}. \

&\textbf{Step 2：打分与注意力权重} \ &\quad \text{对于每个头，注意力权重为：} \ &\quad \text{Scores}^{(i)} = \frac{Q^{(i)} (K^{(i)})^\top}{\sqrt{d_k}} \in \mathbb{R}^{n \times m}, \ &\quad A^{(i)} = \text{softmax}(\text{Scores}^{(i)}) \in \mathbb{R}^{n \times m}. \

&\textbf{Step 3: 拼接矩阵加速}\ &\quad 在实践中会使用W_Q = [[W_Q^1],[W_Q^2],\cdots,[W_Q^h]]\in \mathbb{R}^{d_{model}\times h\cdot d_k}拼接出来. \ &\quad 同理W_K\in\mathbb{R}^{d_{model}\times h\cdot d_k},\quad W_V\in \mathbb{R}^{d_{model}\times h\cdot d_v}.\ &\quad 之后再拆分Q\to(h,n,d_k​),\quad K\to(h,m,d_k​),\quad V\to(h,m,d_v​)\ &\quad \text{Scores}=\frac{QK^T}{\sqrt{d_k}}\in \mathbb{R}^{h\times n\times m}. \ &\quad \text{A}=\text{softmax}(\text{Scores})\in\mathbb{R}^{h\times n\times m}\

&\textbf{Step 4：加权求和得到每个头的输出} \ &\quad O^{(i)} = A^{(i)} V^{(i)} \in \mathbb{R}^{n \times d_v}. \ &\quad 拼接矩阵的 O = AV\in\mathbb{R}^{h\times n\times d_v} \

&\textbf{Step 5：拼接所有头并做最终线性变换} \ &\quad \text{将 $h$ 个头的结果拼接：} \ &\quad O = \text{Concat}(O^{(1)}, \dots, O^{(h)}) \in \mathbb{R}^{n \times (h \cdot d_v)}. \ &\quad 拼接矩阵的O\to \mathbb{R}^{n \times (h \cdot d_v)}\

&\quad \text{再用输出投影矩阵：} \ &\quad W_O \in \mathbb{R}^{h \cdot d_v \times d_{\text{model}}}, \ &\quad \text{得到最终输出：} \ &\quad \text{MHA}(X) = O W_O \in \mathbb{R}^{n \times d_{\text{model}}}. \end{aligned} $$ 注意：在handout中由于torch等库表示向量维度方式不同，可能有维度与上文所写的相反的情况。

在mask的时候，注意$\text{Score}\in \mathbb{R}^{h\times n\times m}$，其中n是解码的句子长度，m是输入的句子长度。在encoder时候，两者同长为seq_len，在decoder的时候不相同，m是encoder输入，n是decoder自回归输入。但是可以用padding使两者同长。至于为什么要把mask在自注意机制中写死，我也不是很清楚，理论上decoder需要mask机制是因为decoder需要自回归不断预测下一个词，所以在训练的时候要mask防止看到下一个词，而encode是不需要的，这是因为现在的llm并非原始Transformer模型，而是纯decoder模型，满足一个自回归的chatbot的任务需求。而原始Transformer则是进行翻译任务，需要提供原文和翻译，因此设计了encoder和decoder。

同时要求对$A$的每个头的query和key向量加上rope position embedding。

The Full Transformer LM

完成了所有子层后，就可以着手组装完整的大语言模型。

最后通过一个归一化和线性网络。 写完整个模型架构之后只能感叹“好的研究是超出时代的”。

训练大语言模型

训练一个大语言模型主要需要三个部分：

• 损失函数：我们需要定义一个交叉熵损失函数
• 优化器(Optimizer)：定义一个优化器来最小化损失函数(AdamW)
• 训练循环：我们需要元件来装载数据，保存保存点以及管理训练

交叉熵损失